Интерполяционные многочлены Гаусса строятся для значений x, находящихся в середине таблицы.
Первая формула Гаусса.
Первая формула Гаусса получается, в случае если в качестве узлов интерполяции выбраны
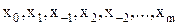
,
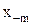
при n=2m+1 (последний узел отбрасывается, в случае если n=2m).
Формула Ньютона с поделёнными разностями для таких узлов имеет форму
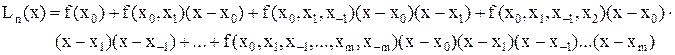
Тут имеются поделённые разности двух типов
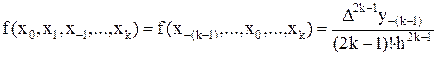
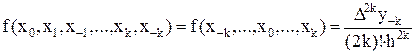
Сделаем замену
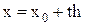
, тогда
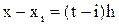
, первая формула Гаусса примет вид
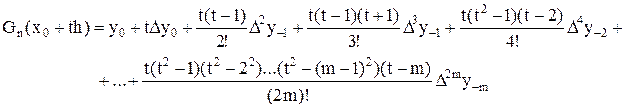
где
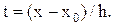
Вторая формула Гаусса.
Вторая формула строится кроме этого как первая, лишь выбраны узлы
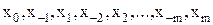
.
Для таких узлов формула Ньютона с поделёнными разностями имеет форму
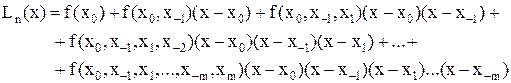
Сделаем ту же замену
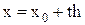
, и вторая формула Гаусса примет вид
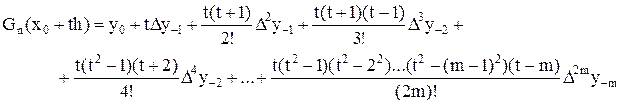
Формулы Гаусса применяют конечные разности, лежащие вблизи горизонтали, проходящей через
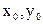
. Эти разности именуются центральными.
Отметим еще раз, что разные интерполяционные многочлены, выстроенные для одного комплекта узлов, являются разными формами записи одного и того же многочлена.
Выстроим таблицу конечных разностей, и отметим на ней, какие конкретно конечные разности употребляются в разных интерполяционных формулах
Оптимальный выбор узлов интерполяции.
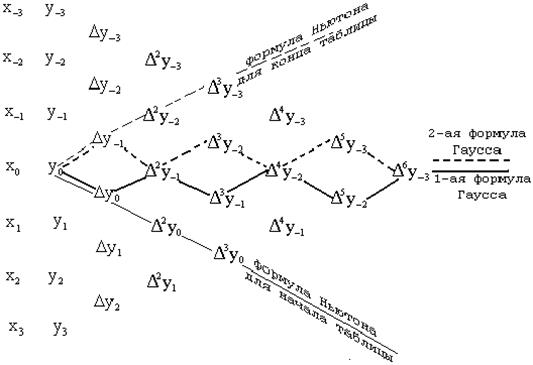
В случае если значения функции
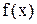
получаются посредством трудоемкого расчета, то возможно поставить вопрос о вычислении значений
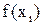
в таких узлах
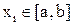
, дабы в оценке погрешности интерполяции
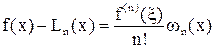
для многочлена
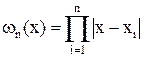
выполнялось условие
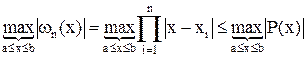
,
где
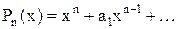
произвольный многочлен степени
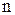
с коэффициентом при старшей степени
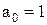
.
Такие многочлены существуют, они с точностью до множителя совпадают с многочленами Чебышева и именуются наименее уклоняющимися от нуля.
Многочлены Чебышева.
Многочлены Чебышева нулевой и первой степени имеют вид
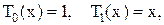
а многочлены n — ой степени выписываются посредством рекуррентной формулы
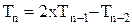
.
Легко продемонстрировать (посредством математической индукции), что
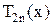
— четная функция, а
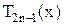
— нечетная. Из рекуррентной формулы направляться, что коэффициент при старшей степени
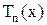
, n1 равен
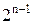
.
У многочлена Чебышева
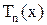
существует n разных вещественных корней, каковые находятся на отрезке
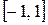
. Дабы отыскать эти корни, запишем
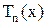
на
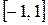
в виде
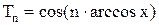
.
Для корней для того чтобы многочлена получаются формулы
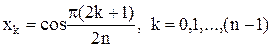
,
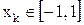
.
Экстремумы многочлена Чебышева достигаются в точках
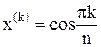
,
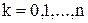
,
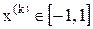
, причем
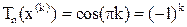
.
Сравним произвольного модулей многочлена
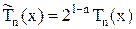
и значения многочленов
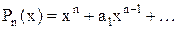
. У обоих этих многочленов коэффициенты при старших степенях равны единице.
Лемма. В случае если
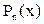
— произвольный многочлен степени n с коэффициентом при старшей степени равным единице, то
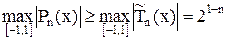
Подтверждение. Предположим неприятное, пускай
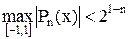
. Степень многочлена
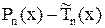
не выше (n-1) (старшие степени уничтожаются). В силу предположения, он не равен нулю тождественно. В случае если
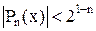
для любого
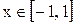
, то символ разности
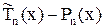
в точках экстремума многочлена Чебышева
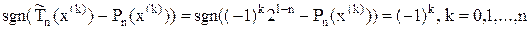
сходится со знаком
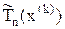
.
Это указывает, что многочлен
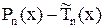
меняет символ на отрезке
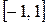
в (n+1)–ой точке, т.е. имеет n корней. Хороший от нуля многочлен степени не более (n-1) не имеет возможности иметь n корней. Взяли несоответствие, лемма доказана.
Увидим, что многочлены
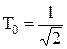
,
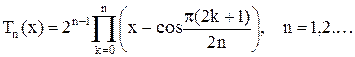
, .
образуют на отрезке
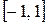
ортонормированную с весом
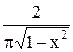
совокупность многочленов, т.е.
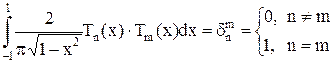
Сделаем замену
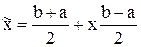
, тогда, в случае если
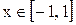
, то
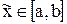
. Корням
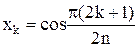
,
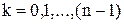
полинома
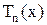
на отрезке
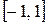
, отвечают точки
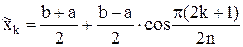
на отрезке
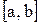
. В случае если эти точки забрать в качестве узлов интерполяции, то
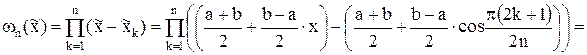
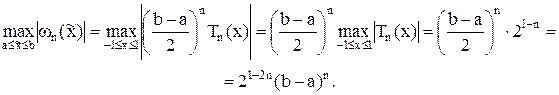
Это указывает, что
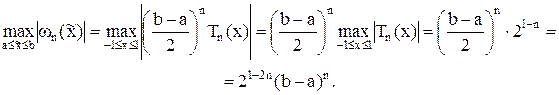
Для выбранных узлов интерполяции получается оценка
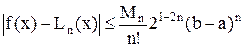
,
и её нельзя улучшить за счет выбора любых вторых узлов.
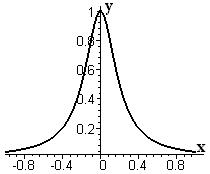
Замечание. На опасность появления громадной погрешности интерполяции обратил внимание в 1901г. Рунге. На отрезке
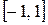
рассматривалась аналитическая функция

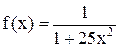
(на рисунке изображен её график).
В случае если при построении интерполяционного многочлена для данной функции, выбрать равноотстоящие узлы, к примеру,
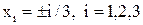
для n=6, то при
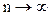
последовательность
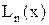
не сходится к
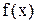
для значений
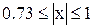
.
В случае если же в качестве узлов выбирать корни полинома Чебышева, то
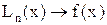
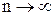
для любого значения
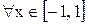
.
Имеется теорема Фабера: в случае если
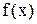
непрерывно дифференцируема (одной непрерывности мало), то интерполяционные многочлены
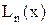
, выстроенные на отрезке
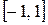
по узлам, совпадающим с корнями многочлена Чебышева, сходятся к
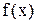
при
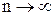
.
Контрольные вопросы.
1. какое количество интерполяционных многочленов степени n-1 возможно выстроить по заданным n узлам?
2. Сформулируйте постановку задачи интерполяции. Что такое экстраполяция?
3. Сформулируйте постановку задачи интерполяции с кратными узлами.
4. Как отличаются друг от друга разные интерполяционные многочлены (Лагранжа, Ньютона, и т.п.), выстроенные по одному и тому же комплекту узлов?
5. Как оценивается погрешность интерполяционного полинома? Как её возможно уменьшить?
6. Как оптимальным образом выбрать узлы интерполяции?
7. Перечислите свойства поделённых разностей.
8. Перечислите свойства конечных разностей.
9. Для каких функций погрешность интерполяции равна нулю?
10. Пускай задана громадная таблица значений функции. Как размещение значения х воздействует на выбор интерполяционной формулы? Как наилучшим образом выбрать степень интерполяционного многочлена?
Упражнения
3. Пускай
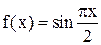
, выстройте интерполяционный многочлен
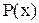
, совпадающий с функцией
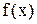
в точках x=0, x=1, x=2. Оцените
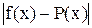
на отрезке
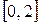
. Сравните эту оценку с фактической погрешностью в точке x=1/2 (либо x=3/2)
4. Пускай
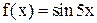
,
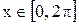
. Выясните ход h таблицы значений
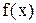
, дабы линейная интерполяция (многочлен
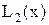
) снабжала точность
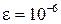
.
5. Пускай на отрезке
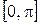
заданы значения функции
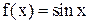
в узлах
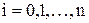
,
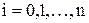
(
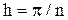
). Выясните, при каком значении числа n для интерполяционного многочлена
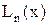
будет выполняться оценка
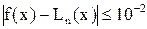
для любого
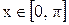
.
6. На сетке
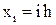
,
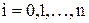
,
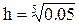
заданы значения
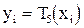
, где
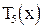
– многочлен Чебышева. Вычислите значение
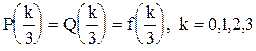
.
7. Выстройте таблицу конечных разностей для таблицы значений функции
| x | -3 | -2 | -1 | ||||
| y | -2.9 | -4 | -3.1 | 4.9 |
Многочленом какой степени разумно интерполировать эту функцию
8. Выстройте интерполяционный многочлен Ньютона третьей степени для точки x=2.7, в случае если функция задана таблично
| x | -3 | -2 | -1 | ||||
| y | 0.1 | -3 | -4 | -3.1 | 5.4 | 11.7 |
9. Пускай
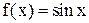
, P(x) и Q(x)– два полинома третьей степени, удовлетворяющие условиям
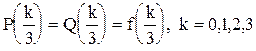
. Оцените для любого
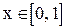
значение
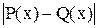
.
10. Пускай дана таблица пятизначных десятичных логарифмов для
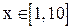
с шагом
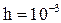
. Будет ли погрешность линейной интерполяции (многочлен
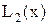
) меньше чем
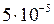
.
11. Выстройте интерполяционный многочлен для функции Рунге
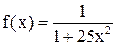
,
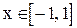
посредством узлов
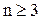
. Оцените погрешность.
12. Заберите любой многочлен степени
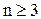
вычислите его значения в (n+2) узлах. Применяйте эти значения для построения интерполяционных многочленов степени n-1, n и n+1. Сравните полученные многочлены с выбранным полиномом
13. Выстройте кусочно–линейную функцию, соответствующую следующим данным
| x | 1/6 | 1/3 | 1/2 | 2/3 | 5/6 | ||
| y | -1 |
14. Выстройте кусочно – квадратичную функцию, соответствующую следующим данных
| x | 1/6 | 1/3 | 1/2 | 2/3 | 5/6 | ||
| y | -1 |
Математика без Ху%!ни. Способ Гаусса. Способ Жордано-Гаусса.





